Часто в физике приходится решать задачи на расчет равновесия в сложных системах, имеющих множество действующих сил, рычагов и осей вращения. В этом случае проще всего использовать понятие момента силы. В данной статье приводятся все необходимые формулы с подробными объяснениями, которые следует использовать для решения задач названного типа.
О чем пойдет речь?

Многие люди наверняка обращали внимание, что если воздействовать с какой-либо силой на предмет, закрепленный в некоторой точке, то он начинает вращаться. Ярким примером может служить дверь в дом или в комнату. Если ее взять за ручку и толкнуть (приложить силу), то она начнет открываться (поворачиваться на петлях). Этот процесс представляет собой проявление в быту действия физической величины, которая получила название момента силы.
Из описанного примера с дверью следует, что рассматриваемая величина указывает на способность силы совершать вращение, что является ее физическим смыслом. Также эту величину называют моментом кручения.
Определение момента силы
Перед тем как дать определение рассматриваемой величине, приведем простой рисунок.
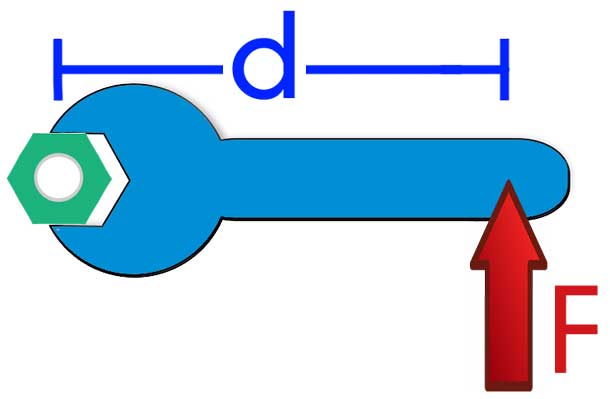
Итак, на рисунке изображен рычаг (синего цвета), который закреплен на оси (зеленый цвет). Этот рычаг имеет длину d, а к его концу приложена сила F. Что будет в этом случае происходить с системой? Верно, рычаг начнет вращаться против часовой стрелки, если смотреть на него сверху (отметим, что если напрячь немного свое воображение и представить, что взгляд направлен снизу на рычаг, то он будет вращаться по часовой стрелке).
Пусть точка закрепления оси называется O, а точка приложения силы - P. Тогда, можно записать следующее математическое выражение:
OP¯* F¯ = M¯FO.
Где OP¯ - это вектор, который направлен от оси к концу рычага, он также называется рычагом силы, F¯ - это вектор приложенной силы к точке P, а M¯FO - это момент силы относительно точки O (оси). Эта формула является математическим определением рассматриваемой физической величины.
Направление момента и правило правой руки
Выражение выше представляет собой векторное произведение. Как известно, его результатом также является вектор, который перпендикулярен плоскости, проходящей через соответствующие вектора-множители. Этому условию удовлетворяют два направления величины M¯FO (вниз и вверх).
Чтобы однозначно его определить, следует воспользоваться так называемым правилом правой руки. Его можно сформулировать таким образом: если согнуть в полудугу четыре пальца правой руки и направить эту полудугу так, чтобы она шла вдоль первого вектора (первый множитель в формуле) и направлялась к концу второго, тогда оттопыренный вверх большой палец укажет направление момента кручения. Отметим также, что перед тем как использовать это правило, необходимо установить умножаемые вектора так, чтобы они выходили из одной точки (их начала должны совпадать).
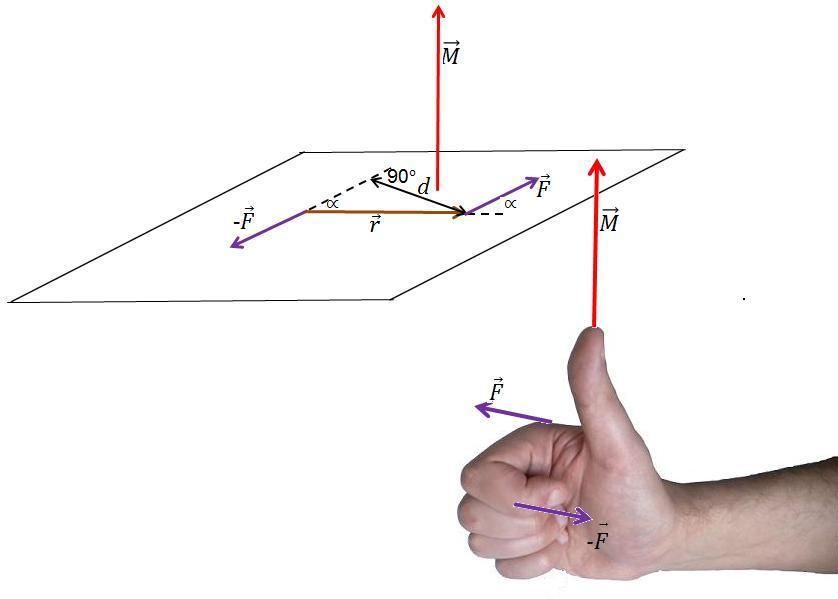
В случае рисунка в предыдущем пункте можно сказать, применив правило правой руки, что момент силы относительно оси будет направлен вверх, то есть на нас.
Помимо отмеченного способа определения направления вектора M¯FO, существует еще два. Приведем их:
- Момент кручения будет направлен таким образом, что если смотреть с конца его вектора на вращающийся рычаг, то последний будет двигаться против хода стрелки часов. Общепринято считать это направление момента положительным при решении разного рода задач.
- Если закручивать буравчик по часовой стрелке, то момент кручения будет направлен в сторону движения (углубления) буравчика.
Все приведенные определения являются эквивалентными, поэтому каждый может выбрать то, которое удобно для него.
Итак, было выяснено, что направление момента силы является параллельным оси, вокруг которой вращается соответствующий рычаг.
Приложенная под углом сила
Рассмотрим рисунок, который приведен ниже.
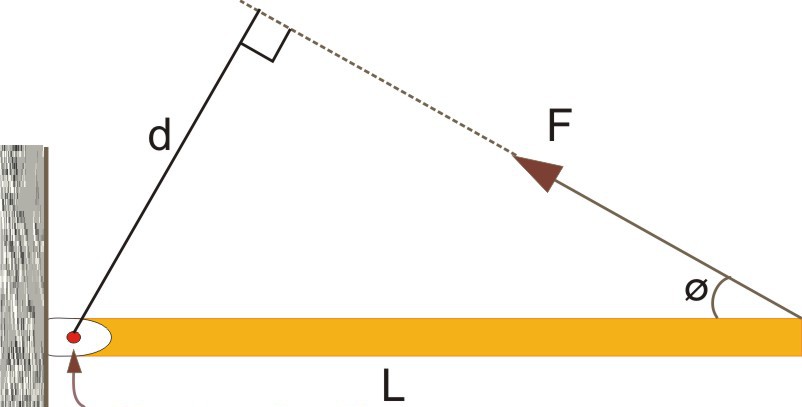
Здесь мы также видим рычаг длиной L, закрепленный в точке (указана стрелкой). На него действует сила F, однако, направлена она под некоторым углом Φ (фи) к горизонтальному рычагу. Направление момента M¯FO в этом случае будет таким же, как и на предыдущем рисунке (на нас). Чтобы вычислить абсолютное значение или модуль этой величины, необходимо воспользоваться свойством векторного произведения. Согласно ему для рассматриваемого примера, можно записать выражение: MFO = L*F*sin(180o-Φ) или, воспользовавшись свойством синуса, перепишем:
MFO = L*F*sin(Φ).
На рисунке приведен также достроенный прямоугольный треугольник, сторонами которого являются сам рычаг (гипотенуза), линия действия силы (катет) и сторона длиной d (второй катет). Учитывая, что sin(Φ) = d/L, указанная формула примет вид: MFO = d*F. Видно, что дистанция d - это расстояние от точки закрепления рычага до линии действия силы, то есть d - рычаг силы.
Обе рассмотренные в этом пункте формулы, которые следуют непосредственно из определения момента кручения, являются полезными при решении практических задач.
Единицы измерения момента кручения
Воспользовавшись определением, можно установить, что величина MFO должна измеряться в ньютонах на метр (Н*м). Действительно, в виде этих единиц она и используется в СИ.
Отметим, что Н*м - это единица измерения работы, которая выражается в джоулях, как и энергия. Тем не менее джоули для концепции момента силы не используют, поскольку эта величина отражает именно возможность осуществления последней. Однако связь с единицей работы имеется: если в результате действия силы F выполнен полный поворот рычага вокруг его точки вращения O, тогда совершенная работа будет равна A = MFO*2*pi (2*pi - угол в радианах, который соответствует 360o). В этом случае единицу измерения момента MFO можно выразить в джоулях на радиан (Дж/рад.). Последняя, наряду с Н*м, также используется в системе СИ.
Теорема Вариньона
В конце XVII века французский математик Пьер Вариньон, изучая равновесие систем с рычагами, впервые сформулировал теорему, которая теперь носит его фамилию. Она формулируется так: суммарный момент нескольких сил равен моменту результирующей одной силы, которая приложена к некоторой точке относительно той же оси вращения. Математически ее можно записать следующим образом:
M¯1+M¯2+...+M¯n = M¯ = d¯*∑ni=1(F¯i) = d¯*F¯.
Эту теорему удобно использовать для расчета моментов кручения в системах с несколькими действующими силами.
Далее приведем пример использования приведенный выше формул для решения задач по физике.
Задача с гаечным ключом
Один из ярких примеров демонстрации важности учета момента силы является процесс откручивания гаек ключом. Чтобы открутить гайку, нужно приложить некоторый момент кручения. Необходимо рассчитать, какую силу следует приложить в точке A, чтобы начать откручивать гайку, если эта сила в точке B равна 300 Н (см. рисунок ниже).
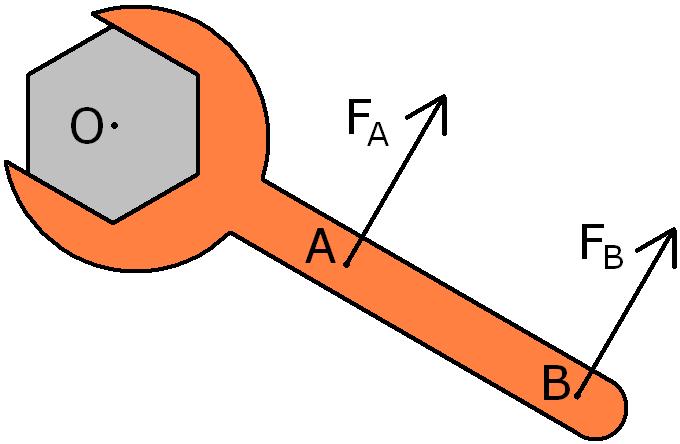
Из приведенного рисунка следуют две важные вещи: во-первых, расстояние OB в два раза больше, чем OA; во-вторых, силы FA и FB направлены перпендикулярно к соответствующему рычагу с осью вращения, совпадающей с центром гайки (точка O).
Момент кручения для этого случая можно записать в скалярной форме так: M = OB*FB = OA*FA. Поскольку OB/OA = 2, то это равенство будет выполняться только тогда, когда FA будет больше FB в 2 раза. Из условия задачи получаем, что FA = 2*300 = 600 Н. То есть, чем больше длина ключа, тем легче откручивать гайку.
Задача с двумя шарами разной массы
На рисунке ниже приведена система, которая находится в равновесии. Необходимо найти положение точки опоры, если длина доски равна 3 метра.

Так как система находится в равновесии, то сумма моментов всех сил равна нулю. На доску действуют три силы (веса двух шаров и сила реакции опоры). Поскольку сила опоры не создает момента кручения (длина рычага равна нулю), то остается только два момента, создаваемых весом шаров.
Пусть точка равновесия находится на расстоянии x от края, где лежит шар массой 100 кг. Тогда можно записать равенство: M1-M2 = 0. Поскольку вес тела определяется по формуле m*g, тогда имеем: m1*g*x - m2*g*(3-x) =0. Сокращаем g и подставляем данные, получаем: 100*x - 5*(3-x) = 0 => x = 15/105= 0,143 м или 14,3 см.
Таким образом, чтобы система находилась в равновесии, необходимо установить опорную точку на расстоянии 14,3 см от края, где будет лежать шар массой 100 кг.



























