Изучение свойств и поведения идеального газа является ключевым моментом для понимания физики этого направления в целом. Рассмотрим в данной статье, что включает в себя концепция идеального одноатомного газа, какими уравнениями описываются его состояние и внутренняя энергия. А также решим пару задач по этой теме.
Общее понятие
Каждый школьник знает, что газ - это одно из трех агрегатных состояний вещества, которое, в отличие от твердого и жидкого, не сохраняет объем. Кроме того, он также не сохраняет свою форму и всегда заполняет полностью предоставленный ему объем. В действительности последнее свойство относится к так называемым идеальным газам.
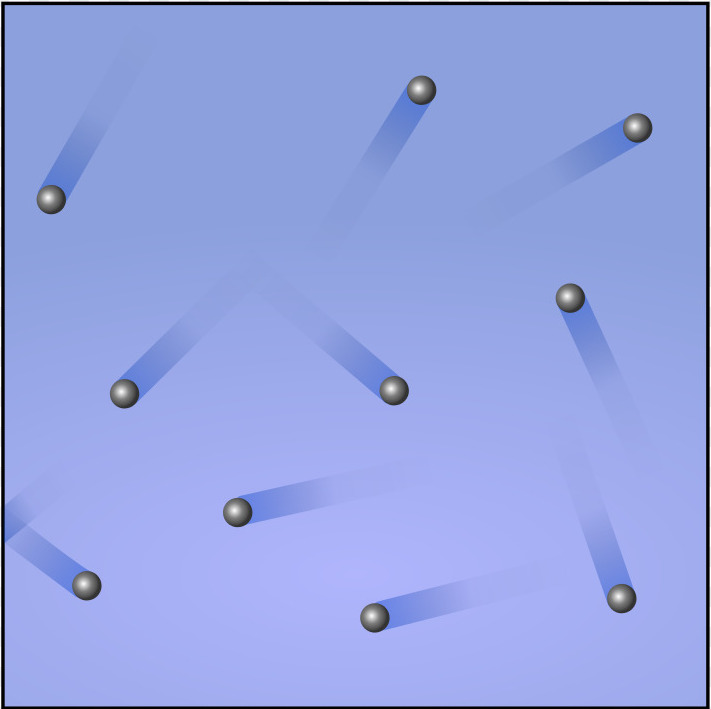
Концепция идеального газа тесно связана с молекулярно-кинетической теорией (МКТ). В соответствии с ней частицы газовой системы движутся хаотически во всех направлениях. Их скорости подчиняются распределению Максвелла. Частицы не взаимодействуют друг с другом, и расстояния между ними намного превышают их размеры. Если все перечисленные условия соблюдаются с определенной точностью, то газ можно считать идеальным.
Любые реальные среды близки по своему поведению к идеальным, если они имеют невысокие плотности и высокие абсолютные температуры. Кроме того, они должны состоять из химически неактивных молекул или атомов. Так, водяной пар из-за присутствия между молекулами H2O сильных водородных взаимодействий не считается идеальным газом, а воздух, состоящий из неполярных молекул, является им.
Закон Клапейрона-Менделеева
Во время анализа, с точки зрения МКТ, поведения газа в равновесии можно получить следующее уравнение, которое связывает основные термодинамические параметры системы:
P * V = n * R * T.
Здесь давление, объем и температура обозначены латинскими буквами P, V и T соответственно. Величина n - это количество вещества, которое позволяет определить число частиц в системе, R - газовая постоянная, не зависящая от химической природы газа. Она равна 8,314 Дж/(К*моль), то есть любой идеальный газ в количестве 1 моль при его нагреве на 1 К, расширяясь, совершает работу 8,314 Дж.
Записанное равенство называется универсальным уравнением состояния Клапейрона-Менделеева. Почему? Названо оно так в честь французского физика Эмиля Клапейрона, который в 30-е годы XIX века, изучая установленные до этого экспериментальные газовые законы, записал его в общем виде. Впоследствии Дмитрий Менделеев привел его к современной форме, введя константу R.

Внутренняя энергия одноатомной среды
Одноатомный идеальный газ отличается от многоатомного тем, что его частицы обладают всего тремя степенями свободы (поступательное движение вдоль трех осей пространства). Этот факт приводит к следующей формуле средней кинетической энергии одного атома:
m * v2 / 2 = 3 / 2 * kB * T.
Скорость v называется средней квадратичной. Масса атома и постоянная Больцмана обозначена как m и kB соответственно.
Согласно определению внутренней энергии, она представляет собой сумму кинетической и потенциальной составляющих. Рассмотрим подробнее. Так как потенциальной энергией идеальный газ не обладает, то его внутренняя энергия - это энергия кинетическая. Какова ее формула? Рассчитывая энергию всех частиц N в системе, получим следующее выражение для внутренней энергии U одноатомного газа:
U = 3 / 2 * n * R * T.
Примеры по теме
Задача №1. Идеальный одноатомный газ переходит из состояния 1 в состояние 2. Масса газа при этом остается постоянной (закрытая система). Необходимо определить изменение внутренней энергии среды, если переход является изобарным при давлении, равном одной атмосфере. Дельта объема сосуда с газом составила три литра.
Выпишем формулу для изменения внутренней энергии U:
ΔU = 3 / 2 * n * R * ΔT.
Воспользовавшись уравнением Клапейрона-Менделеева, это выражение можно переписать в виде:
ΔU = 3 / 2 * P * ΔV.
Давление и изменение объема нам известно из условия задачи, поэтому остается перевести их значения в СИ и подставить в формулу:
ΔU = 3 / 2 * 101325 * 0,003 ≈ 456 Дж.
Таким образом, когда одноатомный идеальный газ переходит из состояния 1 в состояние 2, его внутренняя энергия возрастает на 456 Дж.
Задача №2. Идеальный одноатомный газ в количестве 2 моль находился в сосуде. После изохорного нагрева его энергия возросла на 500 Дж. Как изменилась при этом температура системы?
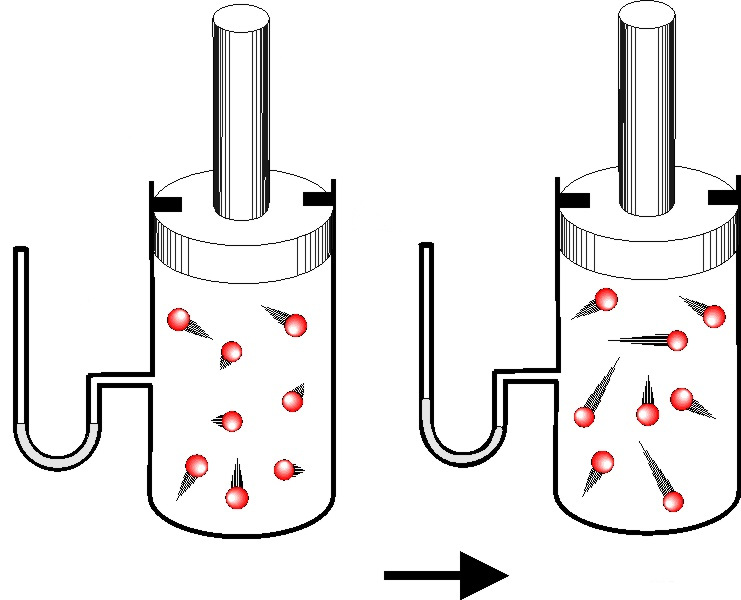
Снова выпишем формулу для изменения величины U:
ΔU = 3 / 2 * n * R * ΔT.
Из нее несложно выразить величину изменения абсолютной температуры ΔT, имеем:
ΔT = 2 * ΔU / ( 3 * n * R ).
Подставляя данные для ΔU и n из условия, получаем ответ: ΔT = +20 К.
Важно понимать, что все приведенные расчеты справедливы только для одноатомного идеального газа. Если система образована многоатомными молекулами, то формула для U уже будет не верна. Закон Клапейрона-Менделеева справедлив для любого идеального газа.



























