Когда в физике описывают движение тел, то используют такие величины, как сила, скорость, путь перемещения, углы поворота и так далее. В этой статье речь пойдет об одной из важных величин, которая объединяет уравнения кинематики и динамики движения. Рассмотрим подробно, что такое полное ускорение.
Понятие об ускорении
Каждый любитель современных скоростных марок автомобилей знает, что одним из важных параметров для них является разгон до определенной скорости (обычно до 100 км/ч) за некоторое время. Этот разгон в физике называют "ускорением". Более строгое определение звучит так: ускорение - это физическая величина, описывающая скорость или быстроту изменения во времени самой скорости. Математически это следует записать так:
? = dv¯/dt
Вычислив первую производную по времени от скорости, мы найдем значение мгновенного полного ускорения ?.
Если движение является равноускоренным, тогда ? от времени не зависит. Этот факт позволяет записать значение полного среднего ускорения ?cp:
?cp = (v2¯-v1¯)/(t2-t1).
Это выражение аналогично предыдущему, только значения скоростей тела берутся за гораздо более длительный промежуток времени, чем dt.
Записанные формулы связи скорости и ускорения позволяют сделать вывод касательно векторов этих величин. Если скорость направлена всегда по касательной к траектории движения, то ускорение направлено в сторону изменения скорости.
Траектория движения и вектор полного ускорения
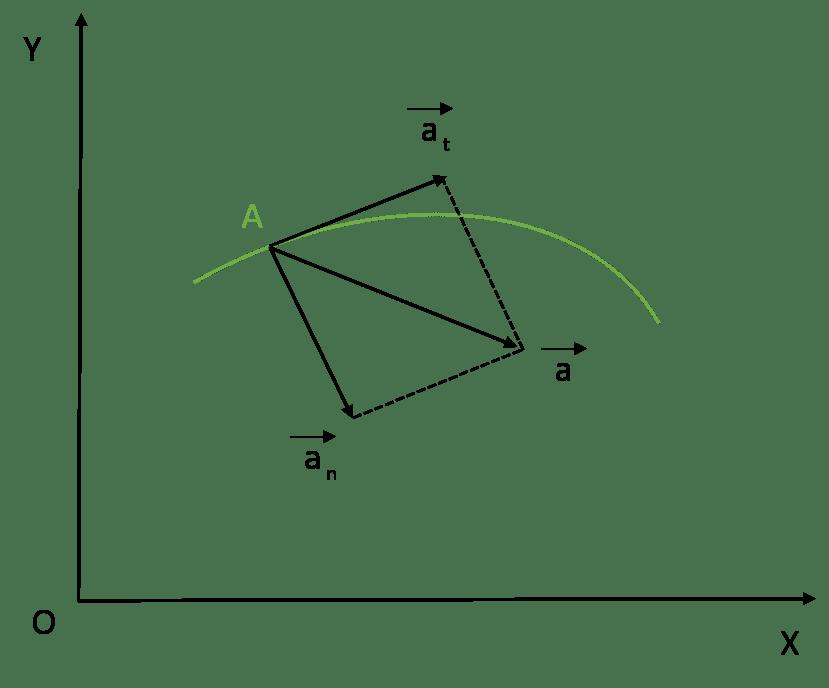
При изучении движения тел следует особое внимание уделять траектории, то есть воображаемой линии, вдоль которой происходит перемещение. В общем случае траектория является криволинейной. При движении по ней скорость тела изменяется не только по величине, но и по направлению. Поскольку ускорение описывает оба компонента изменения скорости, то его можно представить в виде суммы двух составляющих. Чтобы получить формулу полного ускорения через отдельные компоненты, представим скорость тела в точке траектории в следующем виде:
v¯ = v*u¯
Здесь u¯ - единичный касательный к траектории вектор, v - модель скорости. Взяв производную от v¯ по времени, и упрощая полученные слагаемые, приходим к следующему равенству:
? = dv¯/dt = dv/dt*u¯ + v2/r*re¯.
Первое слагаемое представляет собой тангенциальную компоненту ускорения ?, второе слагаемое - это нормальное ускорение. Здесь r - радиус кривизны, re¯ - единичной длины радиус-вектор.
Таким образом, вектор полного ускорения является суммой взаимно перпендикулярных векторов тангенциального и нормального ускорения, поэтому его направление отличается от направлений рассмотренных компонентов и от вектора скорости.
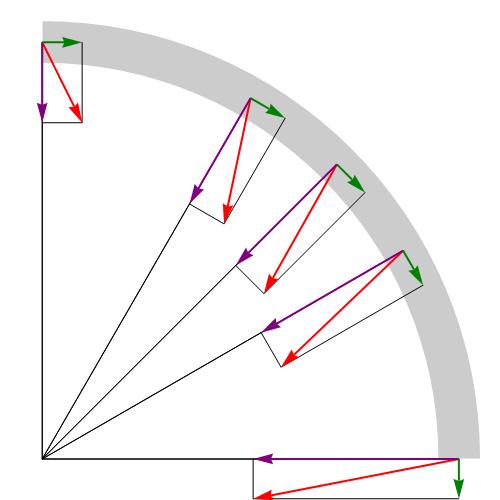
Другим способом определения направления вектора ? является изучение действующих сил на тело в процессе его движения. Величина ? всегда направлена вдоль вектора суммарной силы.
Взаимная перпендикулярность изученных компонент at (тангенциальное) и an (нормальное) позволяет записать выражение для определения модуля полного ускорения:
a = √(at2 + an2)
Прямолинейное ускоренное движение
Если траектория является прямой линией, то изменение вектора скорости в процессе движения тела не происходит. Это означает, что при описании полного ускорения следует знать лишь его тангенциальную компоненту at. Нормальная компонента будет равна нулю. Таким образом, описание ускоренного перемещения по прямой сводится к формуле:
a = at = dv/dt.
Из этого выражения следуют все кинематические формулы прямолинейного равноускоренного или равнозамедленного движения. Запишем их:
v = v0 ± a*t;
S = v0*t ± a*t2/2.
Здесь знак "плюс" соответствует ускоренному движению, а знак "минус" - замедленному (торможение).
Равномерное перемещение по окружности

Теперь рассмотрим, как связаны скорость и ускорение в случае вращения тела вокруг оси. Предположим, что это вращение происходит с постоянной угловой скоростью ω, то есть за равные промежутки времени тело поворачивает на равные углы. При описанных условиях линейная скорость v не изменяет своего абсолютного значения, однако постоянно меняется ее вектор. Последний факт описывает нормальное ускорение.
Выше уже была приведена формула для нормального ускорения an. Запишем ее еще раз:
an = v2/r
Это равенство показывает, что, в отличие от компоненты at, величина an не равна нулю даже при постоянном модуле скорости v. Чем больше этот модуль, и чем меньше радиус кривизны r, тем большее значение приобретет величина an. Появление нормального ускорения обязано действию центростремительной силы, стремящейся удержать на линии окружности вращающееся тело.



























