Все тела, которые окружают нас, находятся в постоянном движении. Перемещение в пространстве тел наблюдается на всех масштабных уровнях, начиная с движения элементарных частиц в атомах вещества и заканчивая ускоренным движением галактик во Вселенной. В любом случае процесс движения происходит с ускорением. В данной статье рассмотрим подробно понятие касательного ускорения и приведем формулу, по которой его можно рассчитать.
Кинематические величины
Прежде чем вести разговор о касательном ускорении, рассмотрим, какими величинами принято характеризовать произвольное механическое перемещение тел в пространстве.
В первую очередь — это путь L. Он показывает, какое расстояние в метрах, сантиметрах, километрах и так далее прошло тело за некоторый промежуток времени.
Вторая важная характеристика в кинематике — это скорость тела. В отличие от пути, она является величиной векторной и направлена вдоль траектории движения тела. Скорость определяет быстроту изменения пространственных координат во времени. Формула для ее вычисления имеет вид:
v¯ = dL/dt
Скорость - это по времени производная пути.
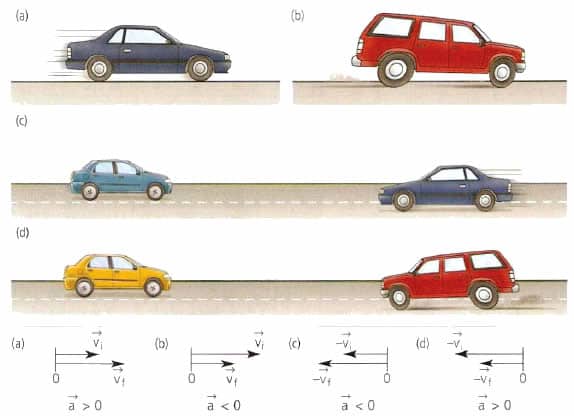
Наконец, третьей важной характеристикой движения тел является ускорение. Согласно определению в физике, ускорение — это величина, которая определяет изменение скорости от времени. Формулу для него можно записать в виде:
a¯ = dv¯/dt
Ускорение, как и скорость, тоже является величиной векторной, однако в отличие от нее оно направлено в сторону изменения скорости. Направление ускорения также совпадает с вектором результирующей силы, оказывающей действие на тело.
Траектория движения и ускорение

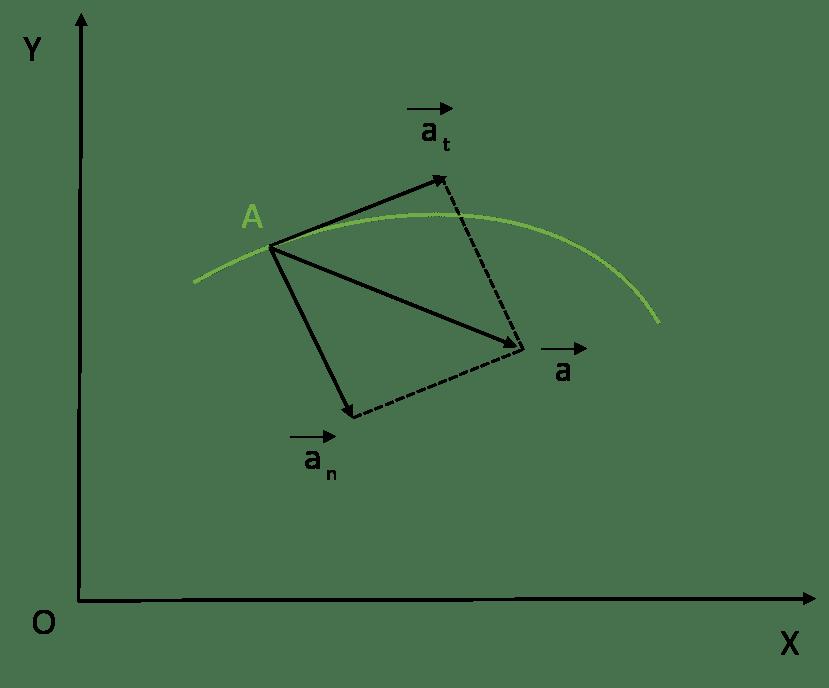
Многие задачи в физике рассматривают в рамках прямолинейного движения. В этом случае, как правило, не говорят о касательном ускорении точки, а работают с линейным ускорением. Однако если перемещение тела не является линейным, то полное его ускорение может быть разложено на две составляющие:
- касательную;
- нормальную.
В случае линейного движения нормальная составляющая равна нулю, поэтому о векторном разложении ускорения не говорят.
Таким образом, траектория движения во многом определяет характер и составные части полного ускорения. Под траекторией движения понимают воображаемую линию в пространстве, вдоль которой тело перемещается. Любая криволинейная траектория приводит к появлению ненулевых компонент ускорения, отмеченных выше.
Определение тангенциального ускорения
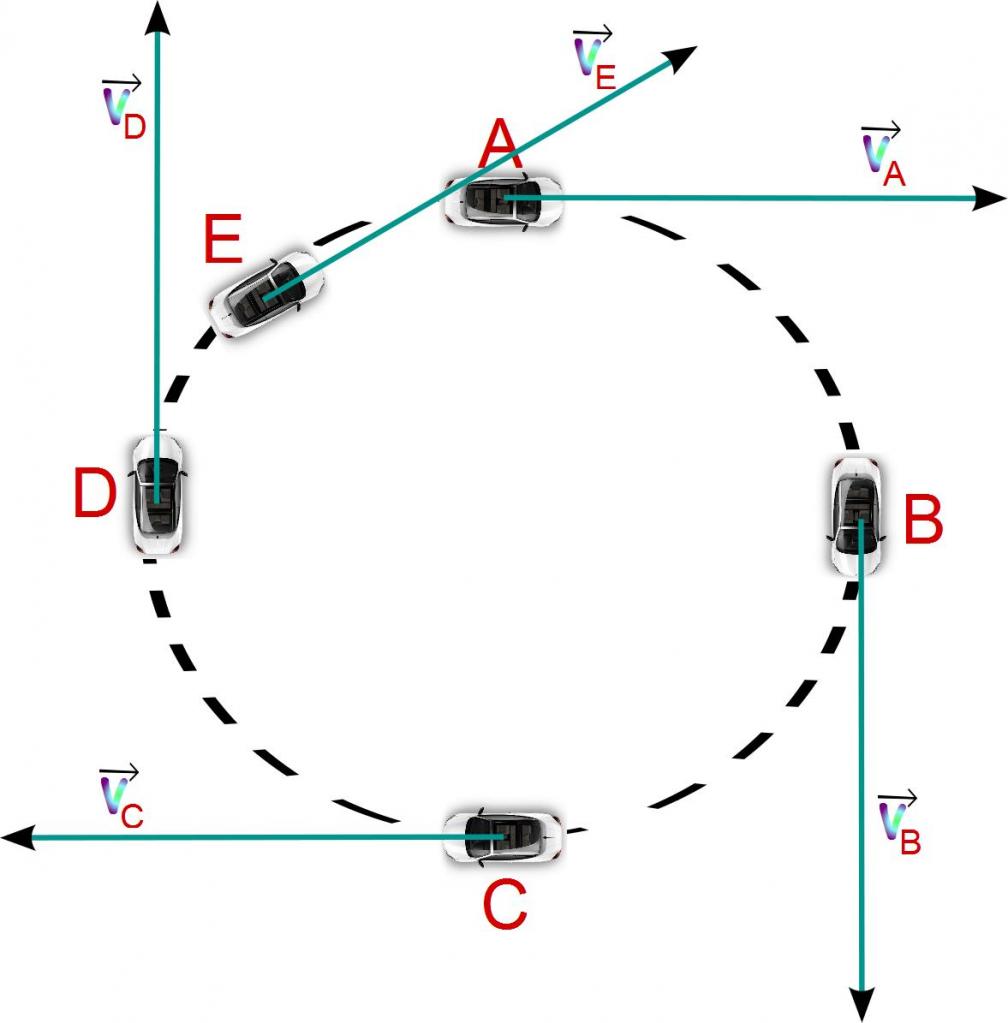
Тангенциальное или, как его еще называют, касательное ускорение — это компонента полного ускорения, которая направлена по касательной к траектории движения. Поскольку вдоль траектории направлена также скорость, то вектор тангенциального ускорения совпадает с вектором скорости.
Выше было дано понятие ускорения как меры изменения скорости. Поскольку скорость - это вектор, то изменить ее можно либо по модулю, либо по направлению. Касательное ускорение определяет только изменение модуля скорости.
Заметим, что в случае прямолинейного движения вектор скорости своего направления не меняет, поэтому, в соответствии с приведенным определением, тангенциальное ускорение и линейное ускорение - это одна и та же величина.
Получение уравнения касательного ускорения
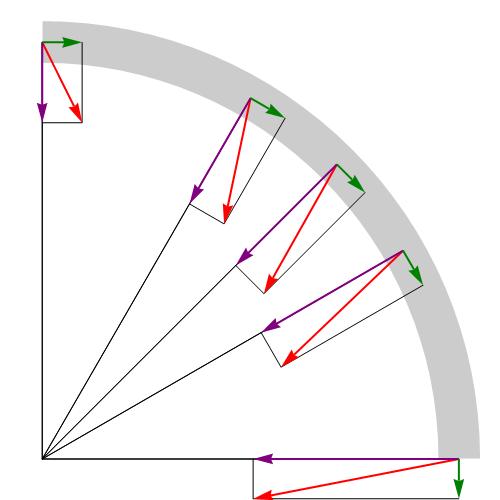
Предположим, что тело движется по некоторой кривой траектории. Тогда его скорость v¯ в выбранной точке можно представить в следующем виде:
v¯ = v*ut¯
Здесь v — модуль вектора v¯, ut¯ — единичный вектор скорости, направленный по касательной к траектории.
Используя математическое определение ускорения, получаем:
a¯ = dv¯/dt = d(v*ut¯)/dt = dv/dt*ut¯ + v*d(ut¯)/dt
При нахождении производной здесь использовалось свойство произведения двух функций. Мы видим, что полное ускорение a¯ в рассматриваемой точке соответствует сумме двух слагаемых. Они являются касательным и нормальным ускорением точки соответственно.
Скажем пару слов о нормальном ускорении. Оно ответственно за изменение вектора скорости, то есть за изменение направления движения тела вдоль кривой. Если явно вычислить значение второго слагаемого, то получится формула для нормального ускорения:
an = v*d(ut¯)/dt = v2/r
Нормальное ускорение направлено вдоль нормали, восстановленной в данную точку кривой. В случае движения по окружности нормальное ускорение является центростремительным.
Уравнение касательного ускорения at¯ имеет вид:
at¯ = dv/dt*ut¯
Это выражение говорит о том, что тангенциальное ускорение соответствует изменению не направления, а модуля скорости v¯ за момент времени. Поскольку тангенциальное ускорение направлено по касательной к рассматриваемой точки траектории, то оно всегда перпендикулярно нормальной компоненте.
Тангенциальное ускорение и модуль полного ускорения
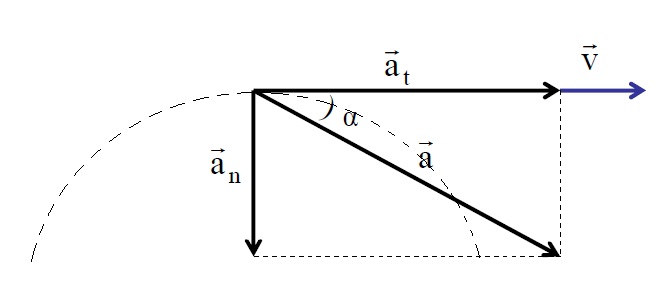
Выше была представлена вся информация, которая позволяет вычислить полное ускорение через касательное и нормальное. Действительно, так как обе компоненты являются взаимно перпендикулярными, то их вектора образуют катеты прямоугольного треугольника, гипотенузой которого является вектор полного ускорения. Этот факт позволяет записать формулу для модуля полного ускорения в следующем виде:
a = √(an2 + at2)
Угол θ между полным ускорением и тангенциальным можно определить так:
θ = arccos(at/a)
Чем больше тангенциальное ускорение, тем ближе оказываются направления касательного и полного ускорения.
Связь касательного и углового ускорения

Типичной криволинейной траекторией, по которой движутся тела в технике и природе, является окружность. Действительно, перемещение шестерен, лопастей и планет вокруг собственной оси или вокруг своих светил происходит именно по окружности. Движение, соответствующее этой траектории, называется вращением.
Кинематика вращения характеризуется теми же величинами, что кинематика движения по прямой, однако, они имеют угловой характер. Так, для описания вращения используют центральный угол поворота θ, угловые скорость ω и ускорение α. Для этих величин справедливы следующие формулы:
ω = dθ/dt;
α = dω/dt
Предположим, что тело совершило один оборот вокруг оси вращения за время t, тогда для скорости угловой можно записать:
ω = 2*pi/t
Линейная скорость в этом случае будет равна:
v = 2*pi*r/t
Где r - радиус траектории. Последние два выражения позволяют записать формулу связи двух скоростей:
v = ω*r
Теперь вычислим производную по времени от левой и правой частей равенства, получим:
dv/dt = r*dω/dt
В правой части равенства стоит произведение углового ускорения на радиус окружности. Левая же часть равенства - это изменение модуля скорости, то есть касательное ускорение.
Таким образом, тангенциальное ускорение и аналогичная угловая величина связаны равенством:
at = α*r
Если предположить, что вращается диск, то тангенциальное ускорение точки при постоянной величине α будет возрастать линейно с увеличением расстояния от этой точки до оси вращения r.
Далее, решим две задачи на применение записанных выше формул.
Определение тангенциального ускорения по известной функции скорости
Известно, что скорость тела, которое перемещается по некоторой кривой траектории, описывается следующей функцией от времени:
v = 2*t2 + 3*t + 5
Необходимо определить формулу касательного ускорения и найти его значение в момент времени t = 5 секунд.
Сначала запишем формулу для модуля тангенциального ускорения:
at = dv/dt
То есть для вычисления функции at(t) следует определить производную скорости по времени. Имеем:
at = d(2*t2 + 3*t + 5)/dt = 4*t + 3
Подставляя в полученное выражение время t = 5 секунд, приходим к ответу: at = 23 м/с2.
Заметим, что графиком скорости от времени в данной задаче является парабола, график же тангенциального ускорения - это прямая линия.
Задача на определение тангенциального ускорения
Известно, что материальная точка начала равноускоренное вращение с нулевого момента времени. Через 10 секунд после начала вращения ее центростремительное ускорение стало равным 20 м/с2. Необходимо определить касательное ускорение точки через 10 секунд, если известно, что радиус вращения равен 1 метр.
Сначала запишем формулу для центростремительного или нормального ускорения ac:
ac = v2/r
Пользуясь формулой связи между линейной и угловой скоростью, получим:
ac = ω2*r
При равноускоренном движении скорость с угловым ускорением связаны формулой:
ω = α*t
Подставляя ω в равенство для ac, получим:
ac = α2*t2*r
Линейное ускорение через тангенциальное выражается так:
α = at/r
Подставляем последнее равенство в предпоследнее, получаем:
ac = at2/r2*t2*r = at2/r*t2 =>
at = √(ac*r)/t
Последняя формула с учетом данных из условия задачи приводит к ответу: at = 0,447 м/с2.



























